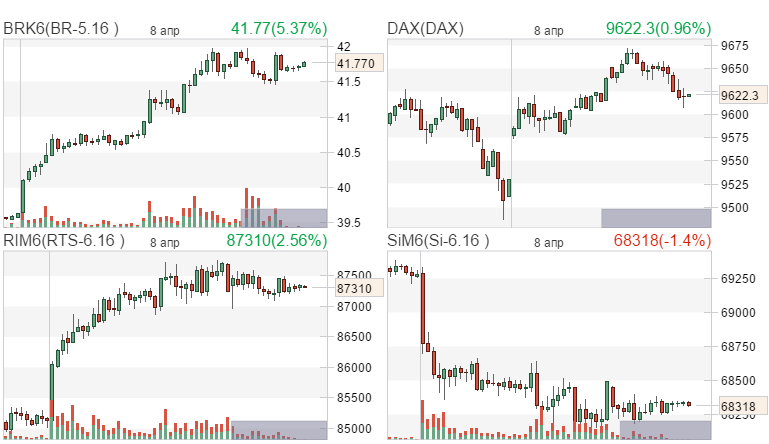
|  |  | |||||||||||
 |
|
||||||||||||
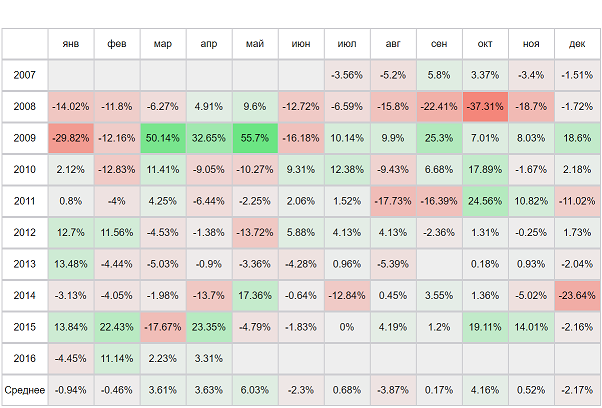
 |  |  | |||||||||||||||
 |
|
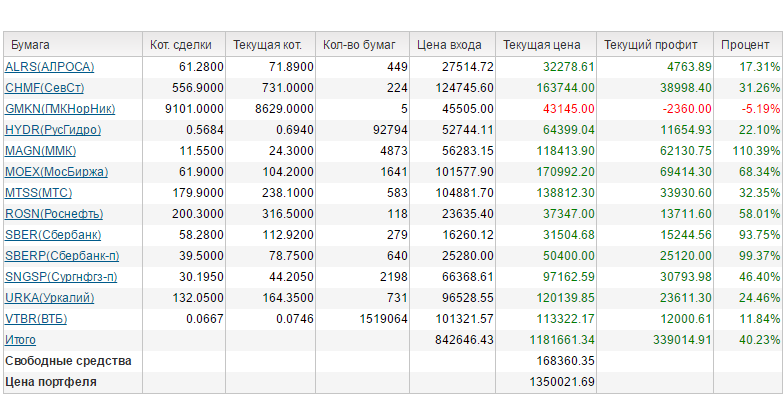
||||||||||||||||
Техническая поддержка
ONLINE
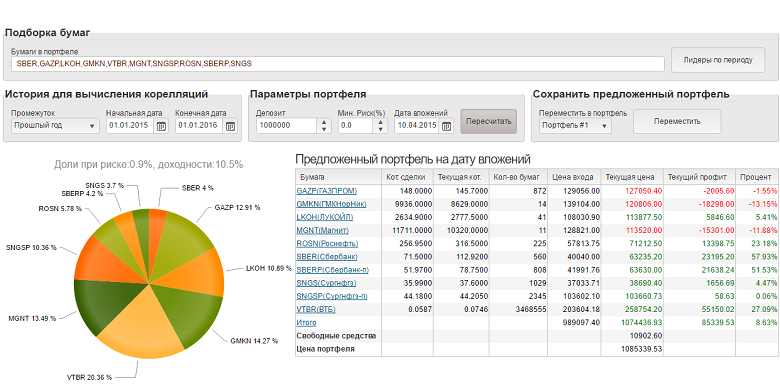
 |  |  | |||||||||||||||||
 |
|
||||||||||||||||||
Inflation Overview | Inflation | Finance & Capital Markets | Khan Academy
ruticker 02.03.2025 23:23:38 Recognized text from YouScriptor channel Khan Academy
Recognized from a YouTube video by YouScriptor.com, For more details, follow the link Inflation Overview | Inflation | Finance & Capital Markets | Khan Academy
Let's say I'm an economist, and I'm curious about whether, in general, things are getting more expensive or not. If they are getting expensive, by how much? The way I'd approach that is by thinking of a bunch of goods and services that the average person would buy. I would think up some type of **basket of goods and services** and try to weight that basket based on how people actually spend their money. So, I'd say, "Okay, 40% of people's money, on average, is spent on housing; maybe another 10% is spent on transportation; maybe another 10% is spent on food." I would go out into the market and see what these things cost, sampling a bunch of products and services to get a decent average. This is not a simple thing to do, but I'm an economist, and I'm serious about trying to calculate that. Let's say that when I take that weighted average of all of this stuff, I come up with a number. I'm not giving you the details of how it's actually calculated, but to give you the idea of what they're doing, I get a number. So, to rent or lease your average automobile, to lease your average apartment, to buy your average servings of food for a given family, let's say I come up with that costs—I'm making up a number here—**$220,000**. My basket of goods and services, just based on the way that I've weighted it, is all happening in **Year 1**. Now, I'm curious whether, between Year 1 and Year 5, things got more expensive. I'll take that same basket of goods and services and try to figure out what its weighted average cost is in Year 5. This is a lot harder than it might sound right now because the baskets of goods and services change. If computers get faster, do you use the same computer, or do you think about what the average computer is, which would now be a better computer? If most people's TVs got bigger, do you use the same TV in Year 1 and Year 5, or do you adjust for what is now the average TV, which is now bigger? If houses have gotten bigger on average, do you use the same house, or do you use the average house? There are a whole bunch of areas here that you can really tweak, and these are actually huge subjects of debate on what the actual increase in cost is. But let's say that you're able to do this in what you think is a pretty reasonable way, and you find that the same basket of goods, adjusted for things like technology and all the rest, now costs **$242,000**. So, your takeaway from here is that the same things that cost **$220,000** in Year 1—the things that gave you the same standard of living—now require you to spend **10% more**. It's gotten **$22,000** more expensive off of **$220,000**, so it's gotten **10% more expensive**. As the economist, you would say that, based on the way you've defined it, your **Consumer Price Index (CPI)** is up by **10%**. Another way, based on the way you measured it, is that price inflation has been **10%** between Year 1 and Year 5. In general, everything got **10% more expensive**, or you would need **10% more money** to have the same standard of living. When people refer to inflation, especially in modern times, they are referring to **price inflation**—this general increase in the price of goods and services measured by some type of basket of goods. There is another type of inflation, and that is **monetary inflation**. Monetary inflation is inflation due purely to an increase in the money supply. In general, if this increase in the money supply does outstrip the productive capacity of the country, it could very well lead to price inflation. But in general, what people measure when they talk about inflation from one year to the next is this basket of goods—they're talking about price inflation. The other thing that you'll sometimes see, maybe in Year 5, is someone saying, "Hey, I could sell you this house." This house in Year 5 is **$660,000**. Someone might ask, "What would be that price if we adjusted it for inflation in Year 1?" What they're saying is, if you adjust for how much value your money has lost—because if things are getting more expensive, that means each dollar is worth less—you can buy less with each dollar. So when people say, "How much is that adjusted for inflation in Year 1 money?" you're essentially saying, "What amount of money would that house have had to cost in Year 1 that, when you adjust it for inflation, you get **$660,000**?" Increasing by **10%** is the same thing as multiplying by **110%** or multiplying by **1.1**. So, what amount of money would that house have had to cost in Year 1 that, if I multiply it by **1.1**, I get **$660,000**? We can do a little quick math here to figure that out. Let's say that I don't know, let's call it **P**. **P** is the price of the house in Year 1. I'll call it **P1**. That times **1.1** is going to be equal to **$660,000** when you factor in the **10% inflation** over these years. This is simple algebra. You can divide both sides by **1.1**, and we get these to cancel out. You get the price of that house in Year 1. **$660,000** divided by **1.1** would give you **$600,000**. If you work this math out, you could figure out the decimals. The general idea is that a house in Year 1 that is **$600,000**, if you factor in the devaluing of the currency or how much more expensive everything got in Year 5, would cost **$660,000**. So, you might hear someone say, when they're talking about inflation or price increases, "This house in Year 5 is **$660,000**, which is equal to **$600,000** in Year 1 money." As an example of that, I live in a neighborhood where the houses have gotten quite expensive. We have neighbors who moved in in the '50s, and they say, "My God, I bought our house for **$10,000**, and now people are selling these houses for so much more." The reality is that it is true—the house has appreciated. But **$10,000** in 1950 was actually a lot of money. Doctors and engineers did not make that much more than that per year. So, the reality is that you have to adjust money for the year that you're talking about, and you have to adjust it for inflation. If you believe the **10% inflation** number, hopefully, people's incomes also increased by the same amount. The same person, maybe with the same skills and the same job, who could afford the house for **$600,000** in Year 1 could now pay **$660,000** for it, and it won't take an unusually large chunk of their expenditure. It would take the same chunk that it did in Year 1. Hopefully, that clarifies things a little bit, and I'll, in the future, do more videos going into the details of inflation.
Залогинтесь, что бы оставить свой комментарий