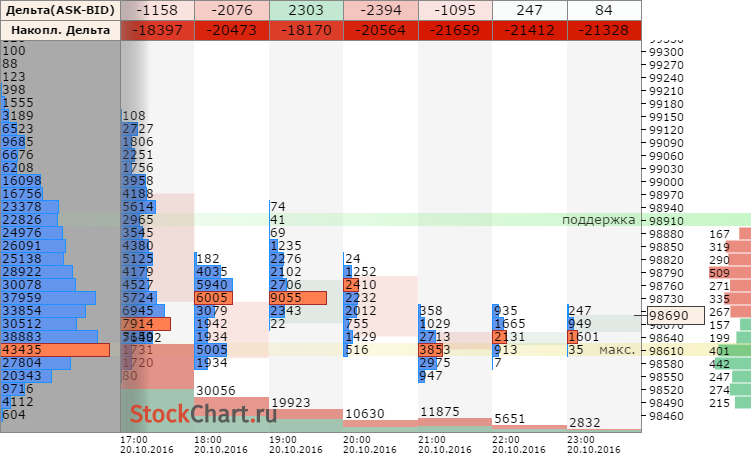
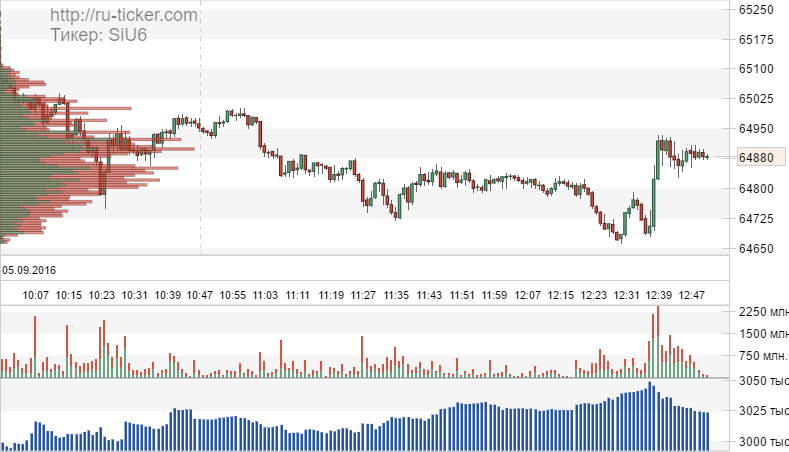
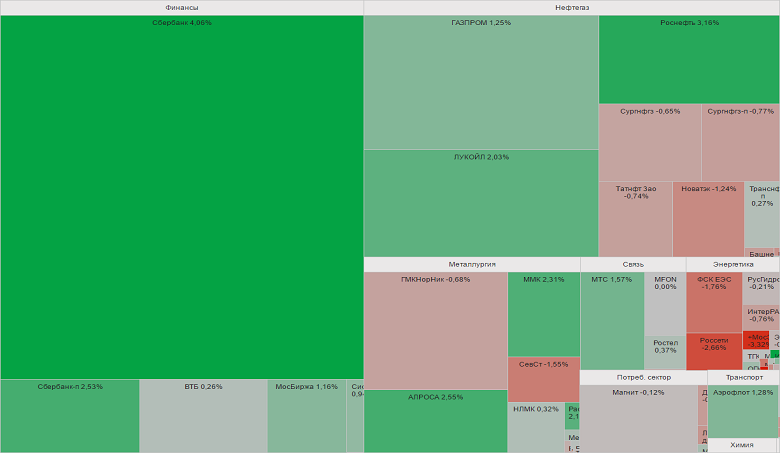
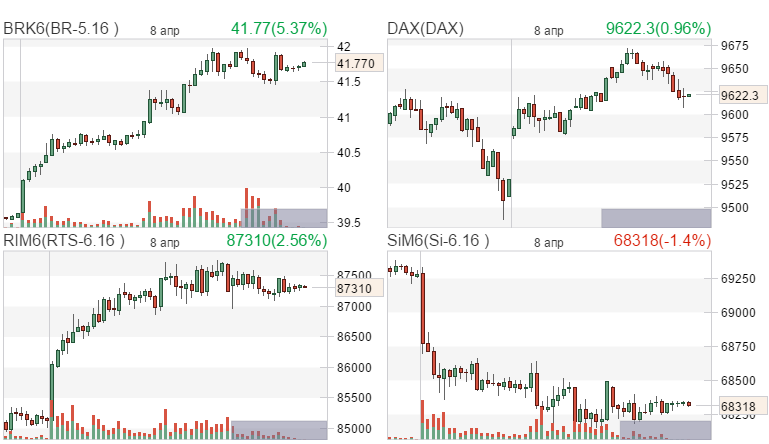
|  |  | |||||||||||
 |
|
||||||||||||
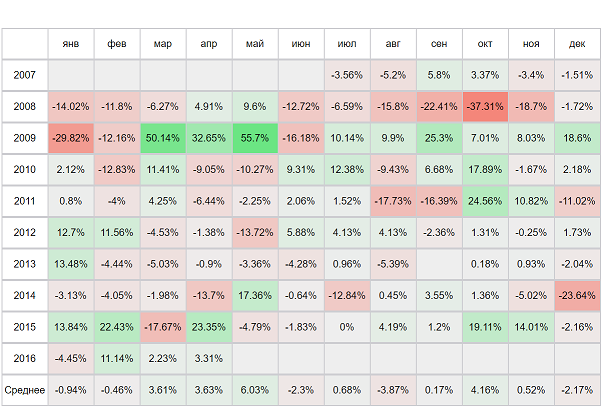
 |  |  | |||||||||||||||
 |
|
||||||||||||||||
Техническая поддержка
ONLINE
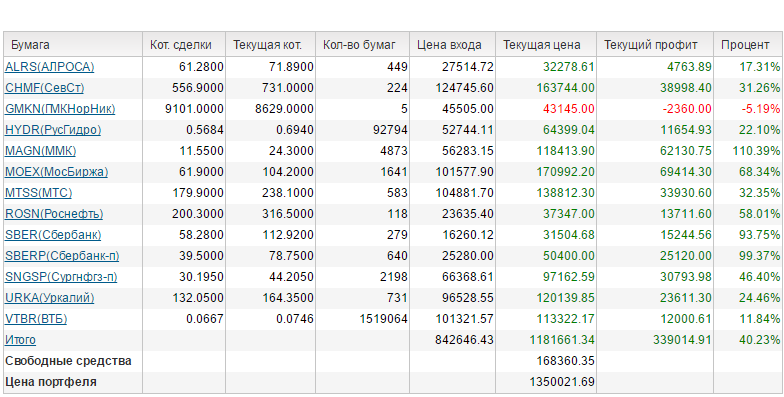
 |  |  | |||||||||||||||||
 |
|
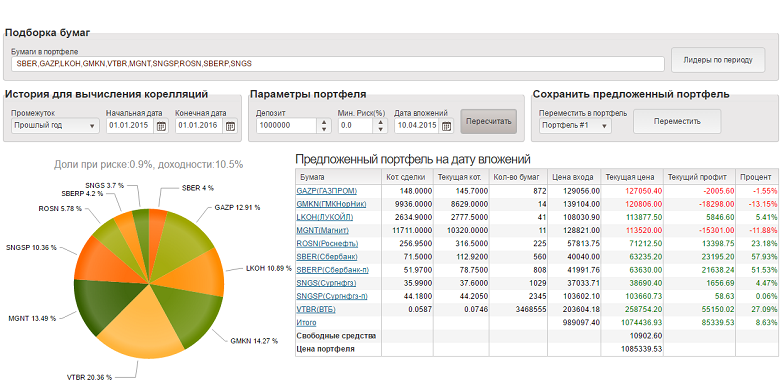
||||||||||||||||||
Intuition behind reverse mode algorithmic differentiation (AD)
ruticker 02.03.2025 12:34:30 Recognized text from YouScriptor channel Joris Gillis
Recognized from a YouTube video by YouScriptor.com, For more details, follow the link Intuition behind reverse mode algorithmic differentiation (AD)
Hello everybody! Today, I'd like to explain **algorithmic differentiation** in an intuitive way. I've prepared a little example for you. So, this is a simple scalar expression that depends on inputs \( x \), \( y \), and \( z \). You could represent this computation in a graph as follows: - This node would mean the multiplication of \( x \) and \( y \). - Here would be the addition of \( x \) and \( y \). - Here, the multiplication of this sub-expression with the \( z \) variable. - Finally, an addition for the last node. **What is the goal of this exercise?** It's to compute the gradient of the expression \( V \). So, the terms you see here are the ones that we are after. Let's start! I'm going to begin with writing some sub-expressions that will help us to understand this expression. I'm introducing intermediate variable \( W_1 \) that is nothing more than \( x \times y \). Intermediate variable \( W_2 \) is \( x + y \), and \( W_3 \) is \( W_2 \times z \). Finally, the expression \( V \) that we want to compute the gradient of is \( W_1 + W_3 \). Now, this is very concrete with multiplications and additions. Let's write it a bit more abstract by writing it as functions. So, in general, we want a binary function here. In this case, a binary function of \( x \) and \( y \). For the second line in our algorithm, we write \( F_2 \); it's again a function of \( x \) and \( y \), but a different one. Again, a function that depends on \( W_2 \) and \( z \). Lastly, we have function \( F_4 \), which depends on \( W_1 \) and \( W_3 \). Let's take the derivative of this. Let's see what we learned back in high school and apply the **chain rule**. First, I'm going to write \( V \) in terms of all these functions. Ok, so \( V \) is function \( F_4 \) with argument \( W_1 \), and \( W_1 \) is \( F_1 \). The second argument of \( F_4 \) is \( W_3 \), so that's given by \( F_3 \) with the first argument being \( F_2(z) \). Close the brackets, so that's the full abstract form of this, and what you see depicted in the graph representation here. **How do we compute the derivative of this total derivative of \( V \)?** The derivative of \( V \) is the partial of \( F_4 \) with respect to its first argument, and I'm inventing this notation with \( B \) to denote the first argument. So, the derivative of \( F_4 \) with respect to the first times the differential of the first input plus the partial of \( F_4 \) with respect to the second times \( F_3 \). Now we can go further and expand these as we go. So, \( F_1 \) in itself is given by the partial of \( F_1 \) with respect to \( P_1 \) times \( dx \) plus the partial of \( F_1 \) with respect to the second argument times \( dy \). This guy, if the total differential of \( F_3 \) is the partial of \( F_3 \) with respect to the first times the total differential of the first argument, which is \( F_2 \), plus the partial of \( F_3 \) with respect to the second argument and \( dz \). So now it's starting to look like this. If we keep the windows, actually there's just one expansion to be done. We will end up with a lot of terms involving either \( dx \), \( dy \), or \( dz \), and if we collect the terms correctly, we end up with these unknown expressions that we're after. Ok, so let's take a look at \( dz \) in this case. So, \( dz \) has a multiplication factor, the partial of \( F_3 \) with respect to the second argument. We can actually see that in the graph. So here is \( C \), and the term I just mentioned is really this guy, and this whole sub-expression is also filled in here. So it's multiplied with the partial of \( F_4 \) with respect to the second argument. So actually, what we could do is just write all these partials at each edge and just bubble upwards from the output to the inputs, collecting all the factors that we encountered. So for \( dz \), we will simply have \( W_4 P_1 \) times the partial of \( F_3 \) with respect to \( P_2 \) that will be here. For \( x \), we can go to roots, so it's this plus this. So concretely, we will have a sum of products. First product: this edge times this edge. Second product: this is this. Ok, so this was the basic route using nothing but the chain rule that we learned in high school. The next part is how to do this in a structured way with **reverse mode** of algorithmic differentiation. In the first block, we've seen how we can use the chain rule to get this gradient, and we can interpret this as bubbling upwards in the expression graph. Just spot the mistake here: we just bubble upwards, going all the possible routes that bring us from the output to the input. Now, going up all possible routes is not really a straightforward algorithm to do, so reverse mode algorithmic differentiation is just a structured way to do this. At least, that's one way to look at it. So, what I'm going to do is introduce intermediate variables for all the nodes and for all the inputs. These intermediate variables I'm going to write with a bar on top of them; that's just convention in our community. **How does it work?** We first do a nominal pass assigning values to all these variables, and then we do a reverse sweep. The reverse sweep starts at the end, naturally. So, this expression is dependent on \( W_1 \) and \( W_3 \), and the information arising from \( V \) is going to bubble upwards towards the nodes \( 1 \) and \( 3 \). So, that's why we're going to say \( W_1 \) bar, which is, as I said, a new intermediate variable that we can use in our algorithm. What we're going to add to this is \( V \) bar times the partial of \( F_4 \) with respect to \( P_1 \), and we have another update to make, and that is \( W_2 \) bar plus equals the street \( V \) coming in and a partial of \( F_4 \) with respect to the second argument. **What does this all mean?** I'm doing an update. It means I have to assign it, and we're actually going to assign all these intermediate bar quantities to zero except for the very last one. So, we have \( V \) bar arriving in and bubbling upwards, and we're just going to put \( V \) bar equal to one. Ok, that's what you need to know to interpret this line. So, this line translates to this. The second line is this, so this operation involves \( W_2 \) and \( z \). So, we're going to have an update rule involving \( W_2 \) bar and \( z \) bar, and we are bubbling up information from the \( W_3 \) variable. Mistake: so we have the partial of \( F_3 \) with respect to \( P_1 \) and \( P_2 \). So, the \( V \) bar has been propagated, and \( W_3 \) has been updated. This information is used again here to arrive at \( W_2 \), and we proceed two times more, and then all information comes up. So, this corresponds to here. Here we have \( X \) bar plus equals, and \( Y \) bar equals to bar partial with respect to one, partial with respect to argument two, right? Last one: \( W_1 \) bar partial of \( F_1 \) with respect to the first argument \( W \) bar \( 1 \) \( W_1 \) bar and the partial with respect to. That's really the gist of reverse mode algorithmic differentiation. So, you initialize bar entities to \( 0 \); only the output \( 1 \) you put to \( 1 \), and then you do a nominal pass and then the reverse pass. You can see from this description that the side of the algorithm here from the nominal pass is kind of copied for the reverse. So, it costs like the cost to compute this gradients is a small multiple of the cost of doing the forward or nominal recipe. So, that's one big advantage of reverse mode algorithmic differentiation. One thing to note is the use of memory. So, when I say here we're bubbling upwards, the partial of \( A_4 \) with respect to \( P_2 \) is actually dependent on these intermediate variables. So, that's why we first need to compute these steps, store these in memory, and later evaluate partials using this sorted data. So, that makes our gradient differentiation or reverse mode memory intensive. There is also a forward mode that has different properties and doesn't use this excessive memory, but reverse mode is much, much cheaper to do gradients of scalar functions. I mean, you can have a million inputs, and just with one reverse sweep, you can get all the gradients for a couple of times the original cost. So, that's what I wanted to tell you today! Hello everybody! Today, I'd like to explain **algorithmic differentiation** in an intuitive way. I've prepared a little example for you. So, this is a simple scalar expression that depends on inputs \( x \), \( y \), and \( z \). You could represent this computation in a graph as follows: - This node would mean the multiplication of \( x \) and \( y \). - Here would be the addition of \( x \) and \( y \). - Here, the multiplication of this sub-expression with the \( z \) variable. - Finally, an addition for the last node. **What is the goal of this exercise?** It's to compute the gradient of the expression \( V \). The terms you see here are the ones that we are after. So let's start. I'm going to begin with writing some sub-expressions that will help us to understand this expression. I'm introducing intermediate variable \( W_1 \) that is nothing more than \( x \times y \). Intermediate variable \( W_2 \) is \( x + y \), and \( W_3 \) is \( W_2 \times z \). Finally, the expression \( V \) that you want to compute the gradient of is \( W_1 + W_3 \). Now, this is very concrete with multiplications and additions. Let's write it a bit more abstract by writing it as functions. In general, we want a binary function here; in this case, a binary function of \( x \) and \( y \). For the second line in our algorithm, we write \( F_2 \); it's again a function of \( x \) and \( y \), but a different one. Again, a function that depends on \( W_2 \) and \( z \). Lastly, we have function \( F_4 \), which depends on \( W_1 \) and \( W_3 \). Let's take the derivative of this. Let's see what we learned back in high school and apply the **chain rule**. First, I'm going to write \( V \) in terms of all these functions. Ok, so \( V \) is function \( F_4 \) with argument \( W_1 \), and \( W_1 \) is \( F_1 \). The second argument of \( F_4 \) is \( W_3 \), so that's given by \( F_3 \) with the first argument being \( F_2(z) \). Close the brackets, so that's the full abstract form of this, and what you see depicted in the graph representation here. **How do we compute the derivative of this?** The total derivative of \( V \) is the partial of \( F_4 \) with respect to its first argument, and I'm inventing this notation with \( B \) to denote the first argument. So, the derivative of \( F_4 \) with respect to the first times the differential of the first input plus the partial of \( F_4 \) with respect to the second times \( F_3 \). Now we can go further and expand these as we go. So, \( F_1 \) in itself is given by the partial of \( F_1 \) with respect to \( P_1 \) times \( dx \) plus the partial of \( F_1 \) with respect to the second argument times \( dy \). This guy, if the total differential of \( F_3 \) is the partial of \( F_3 \) with respect to the first times the total differential of the first argument, which is \( F_2 \), plus the partial of \( F_3 \) with respect to the second argument and \( dz \). So now it's starting to look like this. If we keep the windows, actually there's just one expansion to be done. We will end up with a lot of terms involving either \( dx \), \( dy \), or \( dz \), and if we collect the terms correctly, we end up with these unknown expressions that we're after. Ok, so let's take a look at \( dz \) in this case. So \( dz \) has a multiplication factor, the partial of \( F_3 \) with respect to the second argument. We can actually see that in the graph. So here is \( C \), and the term I just mentioned is really this guy, and this whole sub-expression is also filled in here. So it's multiplied with the partial of \( F_4 \) with respect to the second argument. So actually, what we could do is just write all these partials at each edge and just bubble upwards from the output to the inputs, collecting all the factors that we encountered. So for \( dz \), we will simply have \( W_4 P_1 \) times the partial of \( F_3 \) with respect to \( P_2 \) that will be here. For \( x \), we can go to roots, so it's this plus this. So concretely, we will have a sum of products. First product: this edge times this edge. Second product: this is this. Ok, so this was the basic route using nothing but the chain rule that we learned in high school. The next part is how to do this in a structured way with **reverse mode** of algorithmic differentiation. In the first block, we've seen how we can use the chain rule to get this gradient, and we can interpret this as bubbling upwards in the expression graph. Just spot the mistake here: we just bubble upwards, going all the possible routes that bring us from the output to the input. Now, going up all possible routes is not really a straightforward algorithm to do, so reverse mode algorithmic differentiation is just a structured way to do this. At least, that's one way to look at it. So what I'm going to do is introduce intermediate variables for all the nodes and for all the inputs. These intermediate variables I'm going to write with a bar on top of them; that's just convention in our community. **How does it work?** We first do a nominal pass assigning values to all these variables, and then we do a reverse sweep. The reverse sweep starts at the end, naturally. So this expression is dependent on \( W_1 \) and \( W_3 \), and the information arising from \( V \) is going to bubble upwards towards the nodes \( 1 \) and \( 3 \). So that's why we're going to say \( W_1 \) bar, which is, as I said, a new intermediate variable that we can use in our algorithm. What we're going to add to this is \( V \) bar times the partial of \( F_4 \) with respect to \( P_1 \), and we have another update to make, and that is \( W_2 \) bar plus equals the stream \( V \) coming in and a partial of \( F_4 \) with respect to the second argument. **What does this all mean?** I'm doing an update. It means I have to assign it, and we're actually going to assign all these intermediate bar quantities to zero except for the very last one. So we have \( V \) bar arriving in and bubbling upwards, and we're just going to put \( V \) bar equal to one. Ok, that's what you need to know to interpret this line. So this line translates to this. The second line is this, so this operation involves \( W_2 \) and \( z \). So we're going to have an update rule involving \( W_2 \) bar and \( z \) bar, and we are bubbling up information from the \( W_3 \) variable. Mistake: So we have the partial of \( F_3 \) with respect to \( P_1 \) and \( P_2 \). So the \( V \) bar has been propagated, and \( W_3 \) has been updated. This information is used again here to arrive at \( W_2 \), and we proceed two times more, and then all information comes up. So this corresponds to here. Here we have \( X \) bar plus equals, and \( Y \) bar equals to bar partial with respect to one, partial with respect to argument two, right? Last one: \( W_1 \) bar partial of \( F_1 \) with respect to the first argument \( W \) bar \( 1 \) \( W_1 \) bar and the partial with respect to... That's really the gist of reverse mode algorithmic differentiation. So you initialize bar entities to \( 0 \); only the output \( 1 \) you put to \( 1 \), and then you do a nominal pass and then the reverse pass. You can see from this description that the side of the algorithm here from the nominal pass is kind of copied for the reverse. So it costs like the cost to compute this gradients is a small multiple of the cost of doing the forward or nominal recipe. So that's one big advantage of reverse mode algorithmic differentiation. One thing to note is the use of memory. So when I say here we're bubbling upwards, the partial of \( F_4 \) with respect to \( P_2 \) is actually dependent on these intermediate variables. So that's why we first need to compute these steps, store these in memory, and later evaluate partials using this sorted data. So that makes our gradient differentiation, or reverse mode, memory intensive. There is also a forward mode that has different properties and doesn't use this excessive memory, but reverse mode is much, much cheaper to do gradients of scalar functions. I mean, you can have a million inputs, and just with one reverse sweep, you can get all the gradients for a couple of times the original cost. So that's what I wanted to tell you today!
Залогинтесь, что бы оставить свой комментарий