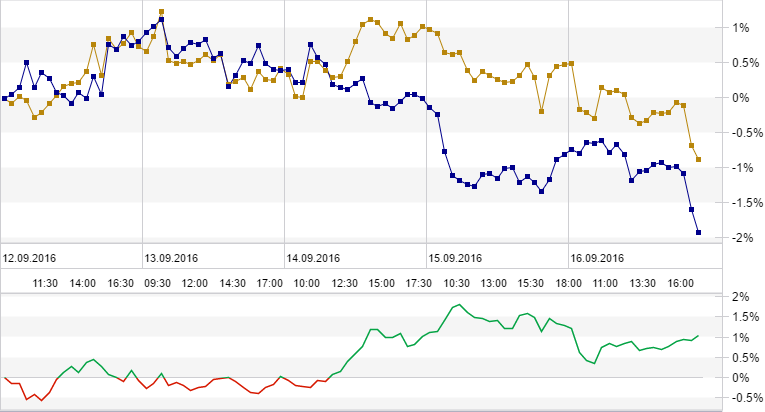
|  |  | |||||||||||
 |
|
||||||||||||
 |  |  | |||||||||||||||
 |
|
||||||||||||||||
Техническая поддержка
ONLINE
 |  |  | |||||||||||||||||
 |
|
||||||||||||||||||
Real and nominal return | Inflation | Finance & Capital Markets | Khan Academy
ruticker 07.03.2025 23:39:00 Recognized text from YouScriptor channel Khan Academy
Recognized from a YouTube video by YouScriptor.com, For more details, follow the link Real and nominal return | Inflation | Finance & Capital Markets | Khan Academy
Let's say last year I put **$100** into some type of savings account in a bank. So, this is a year ago, and now today, exactly one year later, that **$100** has grown to **$110**. If you look at things just in absolute dollar terms, things have grown by **$10**. So, I made **$10** off of an original **$100** investment, which gives me a **10% return**. But what I want to think about is: does this really capture how much more I can buy with this **$110** than I could buy with that **$100** before? Can I really buy **10%** more goods and services today than I could a year ago? To think about that, let's consider a hypothetical inflation rate from last year to this year. Let's say that the inflation ended up being **2%** between a year ago and today. If that's the case, what is **$100** a year ago in today's money? Well, if inflation was **2%**, then **$100** a year ago would buy you the same stuff that **$102** would buy you today. So, what is the dollar return in today's money, in the current purchasing power? We're getting **$110**, and we invested in today's money **$102**. If we look at it from today's terms, we invested something that gives us the same purchasing power as **$102** today, and now it's giving us a purchasing power of **$110**. So, we've gotten **$8** more of purchasing power in today's money. What is the actual real return? Let me write it in for **real return**. We can do it in today's money, and you could do it either way. You could discount the **$110** back to a year ago's money and figure out the real return there, or you can do it in today's money. The real return is: we made **$8** over the course of the year in today's money, and what we originally invested in today's money was **$102**. So, let's get our calculator out: \[ \frac{8}{102} \approx 0.0784 \] This is equal to **7.8%**. So, even though the nominal return—the number if we just look at what we got in exchange for what we invested—was **10%**, because there was **2%** inflation, our actual purchasing power only increased by **7.8%**.
Залогинтесь, что бы оставить свой комментарий