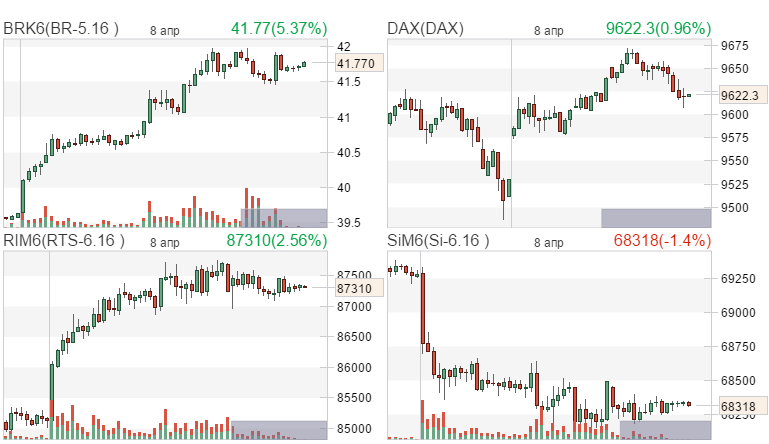
|  |  | |||||||||||
 |
|
||||||||||||
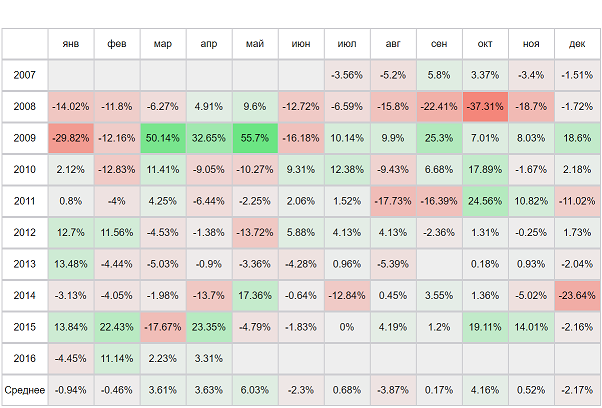
 |  |  | |||||||||||||||
 |
|
||||||||||||||||
Техническая поддержка
ONLINE
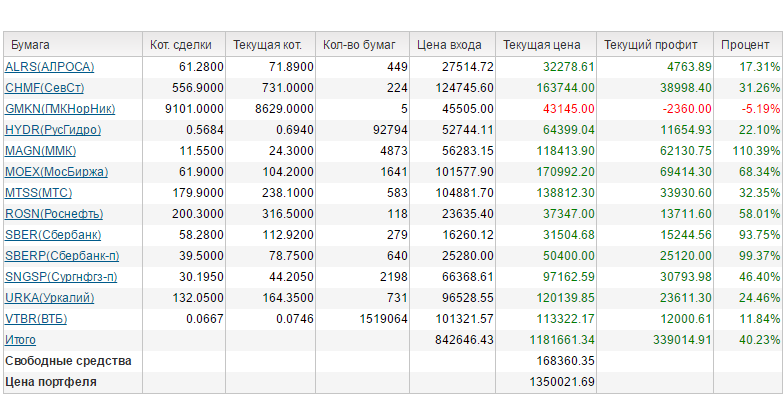
 |  |  | |||||||||||||||||
 |
|
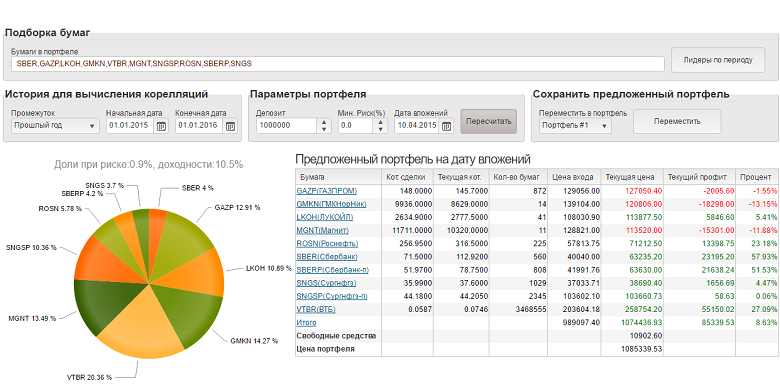
||||||||||||||||||
Relation between nominal and real returns and inflation | Finance & Capital Markets | Khan Academy
ruticker 07.03.2025 23:39:00 Recognized text from YouScriptor channel Khan Academy
Recognized from a YouTube video by YouScriptor.com, For more details, follow the link Relation between nominal and real returns and inflation | Finance & Capital Markets | Khan Academy
Let's generalize the mathematics that we've been doing in the last few videos to calculate the real return, and maybe we'll come up with some interesting formulas or some simple approximations. So, what we've been doing is, at least in the first video, we converted everything to today's dollars. The actual dollar return in today's dollars is the amount that we got, or the net dollar return. The net dollar return is the amount that we originally invested, compounded by the nominal interest rate. Here, we're assuming that we're writing it as a decimal. So, in the example we've been using, it was 10%, and we're going to express this as 0.10. Therefore, this whole value is going to be 1.10. This is how much we're going to get after a year has passed. In our example, this was the $110, which is $100 compounded by 1.1. From that, you want to subtract how much we invested in today's dollars. Well, we originally invested \( p \) a year ago, and in today's dollars, we just need to grow it by the rate of inflation. In the examples we've been doing, we assumed that the rate of inflation is 2%, which would be 0.02. So, this expression right over here is actually the dollar return in today's dollars. It's this value right here that we calculated in the first video. To calculate the real return, we want the dollar return in today's dollars divided by the investment in today's dollars. Once again, this is the investment in today's dollars—the amount we invested originally, grown by inflation. This right over here gives us the real return. Now, one thing we can do right off the bat to simplify this is that we have everything in the numerator and everything in the denominator is divisible by \( p \). So, let's divide the numerator and the denominator by \( p \) to simplify it a little bit, just like that. In the numerator, we get: \[ 1 + n - 1 - 1 + i \] I'll write it like that, still all of that over: \[ 1 + i \] This is equal to \( r \). I'm giving some space here because one simplification I can do here is I can add one to both sides of this equation. So, if I add a one on the right-hand side, I have to add a one on the left-hand side. But a one is the same thing as: \[ \frac{1 + i}{1 + i} \] This is completely identical, and since this is dividing the same thing by itself, this is going to be a one. So, we're adding a one on the left and adding a one on the right. The reason why I did that comes up with the interesting simplification. We have the same denominator here. If I add the numerators \( 1 + i + 1 + n - 1 + i \), these two will cancel out, and we're left with in the numerator just \( y + n \) (the nominal interest rate). In the denominator, we just have \( 1 + 1 + i \), which is equal to \( 1 + \) (the real interest rate). Then, we can multiply both sides by \( 1 + i \). We get an interesting result, and to some degree, this is a common-sense result. I want to show you this is completely consistent with everything we've been doing so far. These terms cancel out, and you get the nominal interest rate, which is the same as growing the real growth, and then that compounded by the rate of inflation, which actually makes a ton of sense.
Залогинтесь, что бы оставить свой комментарий