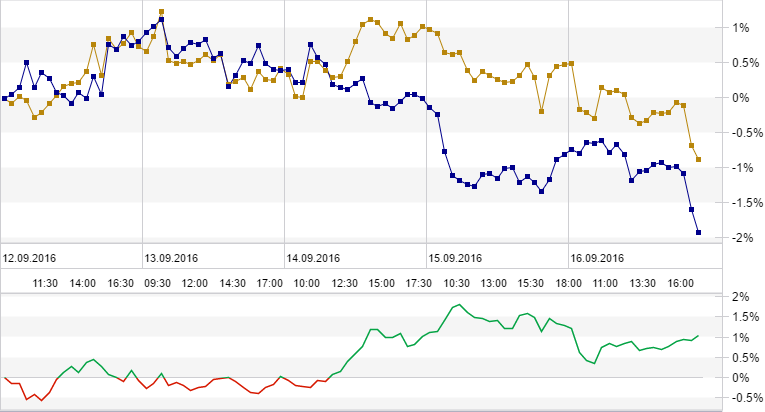
|  |  | |||||||||||
 |
|
||||||||||||
 |  |  | |||||||||||||||
 |
|
||||||||||||||||
Техническая поддержка
ONLINE
 |  |  | |||||||||||||||||
 |
|
||||||||||||||||||
Singlet Fission and Triplet Fusion, René M. Williams, UvA, RE-EDIT
ruticker 04.03.2025 15:24:45 Recognized text from YouScriptor channel René M. Williams
Recognized from a YouTube video by YouScriptor.com, For more details, follow the link Singlet Fission and Triplet Fusion, René M. Williams, UvA, RE-EDIT
# Singlet Fission and Triplet Fusion Hi, my name is **Renee Williams**. I'm an assistant professor at a molecular photonics group at the University of Amsterdam, and today we will discuss **singlet fission** and **triplet fusion**. If you are a novice in this field, you may think, "Singlet fission and triplet fusion? Am I in the wrong lecture?" But you all know about nuclear fission—that's what we use to make energy for our nuclear power plants. You also know about nuclear fusion. In a nutshell, right after the Big Bang, there was just hydrogen. When hot matter started to condense into stars, these nuclei began to fuse. All carbon atoms in your body were made by nuclear fusion in a star. We're all just a bit of stardust! So today, we will discuss singlet fission and triplet fusion. We will take a high-energy excited singlet state and split it into the population of two excited triplet states. Now, in principle, if we can generate electron-hole pairs from these triplets, then we could make very efficient solar cell materials with organic solar cells or even maybe combine it with silicon. **Singlet fission** has the promise of breaking the Shockley-Queisser limit by looking at the mechanism using states, orbitals, and electron spin. Singlet fission is basically one of the methods to create triplets. We will discuss some other methods that also exist. The orientation of the chromophores plays a crucial role in singlet fission; they are very important in how these chromophores are oriented relative to each other. Next, we will discuss singlet fission and the Shockley-Queisser limits. We start off with two molecules or two chromophores in the ground state. We excite one of them to the first excited singlet state, and then we have singlet fission occurring. One goes down to the triplet, while the ground state neighbor molecule goes up to the triplet. In that way, from one photon, we create two triplets that are in the excited states. We can also apply a frontier molecular orbital description. After homolumo excitation, the two electrons depicted in red here redistribute over the system to form two triplet states. However, they are very special triplet states because the spin multiplicity is conserved. These triplet states together have singlet spin multiplicity. The singlet fission process can be described as a double electron transfer, similar to the Dexter mechanism. One electron moves to the other LUMO of the neighboring molecule. This electron in the S0 state moves to the neighbor in the LUMO. The order of these two electron transfer steps is so far unknown; however, the second one is probably less likely than the one discussed before. In theory, we can also get to the final state by promoting one electron from the HOMO to the LUMO, followed by a double electron flip. However, this is not the accepted mechanism. The final state formed, consisting of these two triplets, is a very special pair of triplets, often referred to as a **singlet TT state**. To explain why it is so special, we need to discuss a little more about the fundamentals of triplet states. You all know that electrons have spin; the spin of the electron can be alpha or beta. In the triplet state, we have two unpaired electrons, resulting in four states: alpha-alpha, beta-beta, beta-alpha, and alpha-beta. There are three sublevels without a magnetic field, which we call T_x, T_y, and T_z. If we put the triplet state into a magnetic field, we split the states into the T-minus, T-zero, and T-plus states. This is what we call the so-called **Zeeman effect**. In Amsterdam, we have the Van der Waals Zeeman Institute, named after both Dutch scientists. Similar to the Larmor frequency that you know from proton NMR, we can represent the spin of an electron as it is moving, making a precession movement in the shape of a cone. So here we put everything together: we have one triplet that consists of two alpha spins, one triplet that consists of two beta spins, and this here is what we call the T-zero state. It's the sum of alpha-beta and beta-alpha. It's important to notice that for the T-zero state, there's a phase change relative to the singlet. In the singlet, the arrows that represent the electrons are sort of out of phase. If we take these three triplet states into account, we realize that we are indeed selectively making a specific combination of the two triplets. We can make one triplet that is alpha-beta-beta or one that is beta-alpha-alpha. We only populate two out of nine possibilities. Next to singlet fission, in which we convert one excited singlet state into two triplets, we can also have **triplet fusion**. If two triplets meet each other and interact, they can form an excited singlet and a ground state. This is actually a much more common process that we see in the decay of triplet excited states and also in the interaction of molecular oxygen with excited triplet states. It's normally called **triplet-triplet annihilation**. The two triplets annihilate each other; they kill each other. We will discuss triplet-triplet annihilation another time. What about singlet fission? When can it occur, and what can we use it for? Well, basically, if the singlet excited state has enough energy to populate two triplet states, then you have a driving force. This implies that we need a relatively large singlet-triplet energy gap. The process should, in principle, be independent of the amount of light with which you hit your sample, so it should be independent of laser power or laser fluence. In the bottom left, we see that this singlet-triplet energy gap is actually too small, but on the right, we see that this is a situation where this process can actually happen at high laser power. We can have singlet-singlet annihilation; two singlets can then form a high-energy singlet state, which can split into two triplets. However, this process will be dependent on laser power, so we call this **hot singlet fission**. Singlet fission is a very special way to create triplet excited states. So what are the normal ways to make triplets? In molecules such as acetone and aromatic ketones, which are known for their high triplet yields, the intersystem crossing of the carbonyl group can be viewed as the transfer of charge from the lone pair of the oxygen atom to the carbon atom. This exemplifies the importance of charge transfer in triplet state formation. The orbital magnetic momentum changes when the interacting orbitals are located in different areas of space on a molecule, compensating for the change in spin magnetic momentum of the electron. That's basically **spin-orbit coupling**. The spin-orbit coupling increases strongly with atomic number, so heavier atoms have much stronger spin-orbit coupling. We can have the internal heavy atom effect by, for instance, complexing a molecule to palladium or platinum, creating a metal complex. We can also substitute it with iodine or use the external heavy atom effect by using a solvent that contains iodine, like ethyl iodides. We will discuss spin-orbit coupling and the selection rules for triplet state formation (LCD rules) more extensively another time. Also, in organic light-emitting diodes, triplet state formation occurs due to spin statistics. In fact, 75 percent of triplet excited states are formed due to these charges that are injected into the layer and recombine. However, there are organic LEDs that have more than 25 percent deficiency because these triplet states created in the left material can again annihilate and form a singlet that can emit. Singlet fission is basically the fourth method to create triplet excited states, and it is rather exotic but very interesting. Singlet fission is very interesting for organic solar cells; we can improve the efficiency of these materials by using singlet fission. All the molecules you see here show singlet fission. Joseph Michael has written a very nice review that you can check. Some of these molecules show very inefficient singlet fission on a microsecond time scale because there's not enough driving force; actually, it's endothermic in this case. Some other molecules can show singlet fission on a picosecond time scale, and it is especially the electronic coupling that is important because the mechanism, remember, is double electron transfer. The coupling between the chromophores is very important, and that is also related to the orientation. Especially the work of Michael Wazileski has shown very nicely that the relative orientation of the chromophores is crucial for the singlet fission rate and efficiency. For instance, here on the left and the top right, you see that a particular molecule shows either excimer formation, just like pyrene, or it shows fast singlet fission with a charge transfer mechanism. The orientation of the two chromophoric units is very important for the exact process that is occurring and the rate of the singlet fission. The faster the rate, the more efficient the process can be. By covalently attaching two chromophores, researchers have been able to create what we call **slip-stacked conformers**. The slipping distance of the two chromophores is modulated, which changes the singlet fission efficiency. In stimulated fission, we use one photon to create two excited states. If we can convert these triplet excited states into electron-hole pairs, we can use one photon to create two electrons. This could make organic solar cells more efficient. This implies that with singlet fission, we can break the Shockley-Queisser limits. This limit tells us that at a band gap of about 1.34 electron volts, we can achieve an efficiency of a single-stack solar cell device of about 34 percent. But this is a one photon, one electron process. We can go to higher efficiencies if we manage to apply singlet fission in solar cell materials. There are actually two ways to break the Shockley-Queisser limit: one of them is singlet fission, and the other one is hot charge injection. Shockley actually also invented the transistor, so modern-day computer technology owes a lot to Mr. Shockley. If you want to apply singlet fission to organic solar cells, the fission has to be exergonic. Of course, we have first excitation; the singlet splits into triplets. These triplets should diffuse to the heterojunction, where they can create charges. Mark Baldo from MIT and his group were probably one of the first to show that singlet fission can be really applied to solar cell materials to achieve an efficiency above 100 percent. They used a nice black material, pentacene, as a light absorber. In the crystal packing, the orientation of the molecules is actually quite special. They also performed high-end quantum chemical calculations. They used a stacked device containing P3HT (poly(3-hexylthiophene)), then a layer of pentacene, followed by a layer of C60 and finally a layer of silver. This is the photoactive layer in which all the absorption and significant charge collection occurs. The first thing we see here is that two neighboring pentacene molecules make an angle of about 60 degrees. Photoexcitation creates a singlet excited state, which has a slightly delocalized character. It can split into two triplets, depicted down here, which are actually pretty localized on one molecule. This triplet, if it diffuses to the interface, can dissociate into charges and create photocurrent via this charge transfer state. With this strategy, following co-workers have been able to show an external quantum efficiency of 109 percent. For every photon impinging on the system, they get 1.1 electrons, resulting in a quantum efficiency above one. The layer thickness of the pentacene is a very important factor, and at about 15 nanometers thickness, they achieve optimal conditions. With a relatively thin pentacene layer, they get an efficiency above 100 percent at 670 nanometers. With this strategy, they believe they will be able to combat the Shockley-Queisser limit, especially if they also use low band gap materials that absorb further than 670 nanometers. In conclusion, with singlet fission, we can split a high-energy singlet state into two triplets. However, this triplet state must have a neighboring molecule in the ground state. If this high-energy singlet has more energy than two times the triplet energy, then the process can occur. The orientation of the two interacting chromophores is very important, and either a slip-stacked conformation or an angle of about 60 degrees between the two chromophores seems to be optimal. With singlet fission, we can take one excited state, create two, and convert these two states into two electron-hole pairs. This could allow us to exceed the Shockley-Queisser limit, which would be a significant advancement in the field. In the grand scheme of things, we learned that, also in photochemistry, there are more roads that lead to Rome. Singlet fission is just one of the roads to reach the top of the excited state, and it is a very exotic road. We have also seen before that with pyrene, we can get this excited state dimer—two molecules that interact in the excited state and have an exothermic interaction. For other molecules with the right energetics, they can also interact and display a totally different process: singlet fission, not only the slipped stack conformation. The way these molecules are stacked on each other is very important for the process that is occurring. They can also be stacked on top of each other, like with an angle of about 60 degrees. This is also an example of molecules interacting in the excited state.
Залогинтесь, что бы оставить свой комментарий