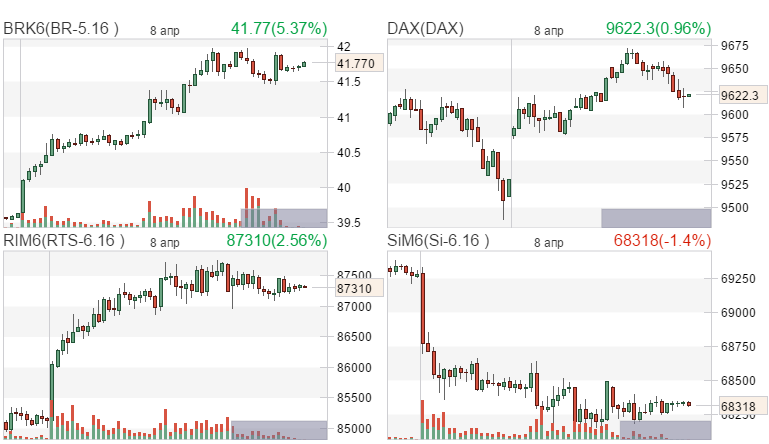
|  |  | |||||||||||
 |
|
||||||||||||
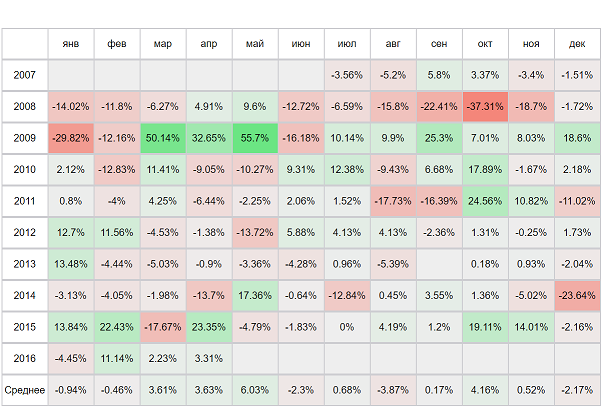
 |  |  | |||||||||||||||
 |
|
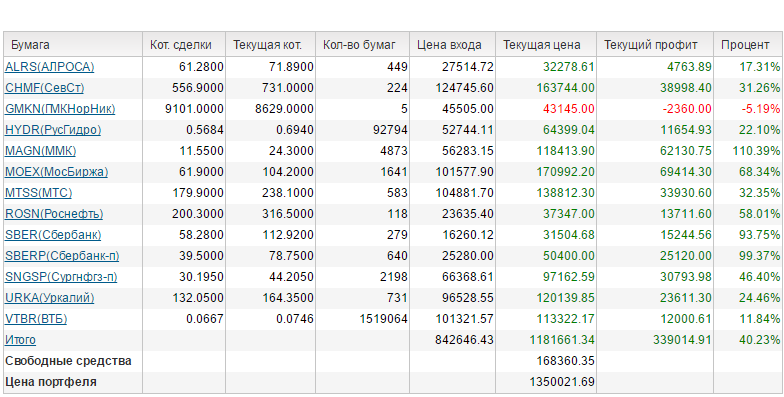
||||||||||||||||
Техническая поддержка
ONLINE
 |  |  | |||||||||||||||||
 |
|
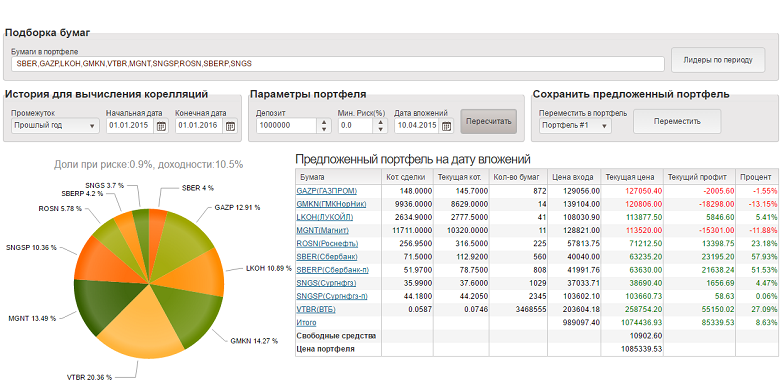
||||||||||||||||||
What is Automatic Differentiation?
ruticker 02.03.2025 12:34:31 Recognized text from YouScriptor channel Ari Seff
Recognized from a YouTube video by YouScriptor.com, For more details, follow the link What is Automatic Differentiation?
Differentiation is everywhere in science and engineering. In machine learning, we need derivatives when we use gradient-based optimization, for example, in **gradient descent**, where we attempt to minimize some objective function by repeatedly tuning our model's parameters in the direction of the negative gradient. In this video, we'll try to understand the basic idea behind **automatic differentiation** (or **autodiff**), a set of techniques that allow us to compute derivatives efficiently. First, let's contrast autodiff with some other ways of computing derivatives. One way we might think to do this, from high school calculus, is to look at our function and manually differentiate it using our basic derivative rules. We could simply code up the result and call it a day, but this can be a fairly tedious process for more complicated functions. We generally prefer an automated approach. Now, automatic differentiation, as its name suggests, is one of these automated approaches, but it's not the only one. Another is **numerical differentiation**, which uses the method of finite differences to approximate derivatives. The simplest version intuitively follows from the limit definition of the derivative. Say we have a scalar-valued function \( f \) for a partial derivative with respect to \( x_i \). We set up a quotient where, in the numerator, we subtract two evaluations of the function at nearby points \( x + h e_i \) and \( x e_i \) (where \( e_i \) is just the unit vector along the \( i \)-axis and \( h \) is a step size, typically a small fraction). While this can be fairly simple to implement, some issues come up with accuracy and numerical stability. One issue is **truncation error**. We're trying to approximate a limit as \( h \) goes to zero, but we're using some non-zero \( h \). What we're really calculating is the slope of a secant line near the tangent line at \( x \). As \( h \) gets closer to zero, the secant line approaches the tangent line, and the truncation error decreases. This eventually leads to what's called **rounding error** due to the limited precision of floating-point arithmetic. So, we have to carefully consider this trade-off between truncation and rounding when selecting a step size. Now, in machine learning, especially in the context of training neural networks, some approximation error may be okay. After all, **stochastic gradient descent** only uses a noisy estimation of the true gradient. The bigger problem with numerical differentiation here is that we need \( O(n) \) evaluations for an \( n \)-dimensional gradient. This time complexity simply won't cut it when we have a model with millions of parameters. Another approach is **symbolic differentiation**, which is essentially an automated version of the manual differentiation we looked at before. We hand a closed-form version of our function to a symbolic differentiation program that applies the standard derivative rules, transforming the original expression into the derivative of interest. This bypasses the sources of error we saw in numerical differentiation, allowing exact computation of derivatives up to numerical precision, but it comes with its own difficulties. One problem is known as **expression swell**, where derivative expressions may be exponentially longer than the original function. Why does this happen? Well, some derivative rules, like the product rule, naturally lead to duplicated computation. Any computation shared between \( f \) and \( f' \) here will be executed twice. If \( f \) itself involved a product of functions, this would be further exacerbated. For example, let's look at this recurrence relation known as the **logistic map**. For \( n = 1 \) and \( 2 \), the derivative expression is about as simple as the original, but as we increase \( n \) further, the derivative quickly gets out of hand. Now, in this example, we can simplify the expression quite a bit to polynomial form, but this isn't always possible. Consider this function known as **soft ReLU**, a common activation function in neural networks. Even two of these composed together leads to a fairly involved derivative. Symbolically differentiating through a network of many layers is usually not tenable. In addition, symbolic differentiation requires our function to be expressed in closed form, limiting our ability to use control flow mechanisms like conditionals, loops, and recursion. **Automatic differentiation** computes derivatives with the same accuracy as symbolic differentiation but operates directly on the program of interest rather than producing an expression for a derivative. The sole intent of autodiff is to obtain its numerical value. It bypasses symbolic inefficiency by leveraging intermediate variables present in the original function's implementation and more easily handles control flow. The basic idea is that ultimately implemented differentiable functions are composed of underlying primitive operations whose derivatives we know, and the **chain rule** allows us to compose these together. There are two main versions of autodiff: **forward mode** and **reverse mode**. We'll first take a look at **forward mode**, the conceptually simpler of the two. Forward autodiff involves augmenting each intermediate variable during the evaluation of a function with its derivative. So instead of individual floating-point values flowing through a function, we can think of these as being replaced by tuples of the original intermediate values (also called **primals**) paired with their derivatives (also known as **tangents**). Say we're interested in this function. We have two scalar inputs \( x_1 \) and \( x_2 \) and a single scalar output. We notice some repeated use of certain sub-expressions, which would likely influence how we implement it. We start with our two input variables, which we'll denote with \( v_{-1} \) and \( v_0 \). As we proceed, we evaluate intermediate variables, some of which will be used more than once in later computations, and we eventually reach the final function output. Now, suppose we'd like to compute the partial derivative of this function with respect to \( x_1 \) at the point \( x_1 = 1.5 \) and \( x_2 = 0.5 \). In addition to the computation of the primals, we simultaneously compute their tangent values. That is, each evaluation of an intermediate variable \( v_i \) will now be accompanied by the value of \( \frac{\partial b_i}{\partial x_1} \). A single pass through the function now produces not only the original output but the partial derivative of interest. This example function only has a single scalar output. Suppose it had multiple outputs. Forward mode autodiff allows us to compute the partial derivatives of each of these outputs with respect to an input variable all in a single forward pass, which is great. The catch is that we have to run a separate forward pass for each input variable of interest. For this example function, we'd have to follow the same procedure again to get partials with respect to \( x_2 \). Consider general functions from \( \mathbb{R}^n \) to \( \mathbb{R}^m \). Each pass of forward mode autodiff produces one column of the corresponding Jacobian. This starts to give us a hint about when we might like to use forward mode. We'll see that relative to reverse mode, forward mode is generally preferred for computing Jacobians where \( n \) is much less than \( m \) (that is, we have few inputs and many outputs). Notice in our example that we initialized \( x \cdot 2 = 1 \) and \( 0 \) since we wanted the partial derivative with respect to \( x_1 \). But partial derivatives are just the axis-aligned special case of more general directional derivatives. We can initialize \( x \cdot \) to any unit vector we'd like and compute the corresponding directional derivative with a single forward pass. More generally, we can actually compute Jacobian-vector products without ever computing the Jacobian matrix itself. We set \( x \cdot \) to the vector of interest and proceed with forward mode autodiff. Now, this seems a little weird, right? After all, we just said that forward mode requires one pass through the function for each input. Well, we can basically think of the Jacobian-vector product as just the Jacobian of a different function: the composition of our original function and one with a single scalar input whose Jacobian is the column vector \( r \). Because the overall Jacobian of this composed function now only has one column, we see why a single forward pass is sufficient. There are several ways to go about actually implementing forward mode autodiff. One route, perhaps the simplest, is to leverage **operator overloading**, where we abstract away the actual derivative computation. Instead of operating on raw floats, we write a simple class with attributes denoting the values of both the primal and its tangent. We could then overload the primitive arithmetic operations to additionally handle derivative computation. For example, for the addition operation, we typically just take the two raw values and add them together. Instead, we'll include the simple sum rule for derivatives and set the dot attribute of the returned object accordingly. We would do the same for the other operators, allowing us to implement the overall function just as we normally would, except this time the values of both the original function and its derivative are produced. Another general route is known as **source code transformation**, where input source code is actually manipulated to produce a new function. This can be more efficient than operator overloading, as it directly exposes the logic of the new source code to the compiler, but it's a bit more difficult to implement. I'll provide links in the description for further details about different kinds of implementations as well as example software libraries. Now, we saw that forward mode autodiff looks like a good route when there are only a few inputs that we're interested in partial derivatives for. But in the context of machine learning, we usually don't meet this condition. In fact, we're typically in the scenario where we have a model with many parameters, even numbering into the billions these days, and we'd like the gradient of a scalar loss with respect to these parameters. **Reverse mode autodiff** allows us to handle this case efficiently. Rather than propagating derivatives forward, they'll be propagated backwards from the output. This is carried out in a two-part process. We first start with a forward pass through the function, evaluating intermediate variables as we did before, but instead of simultaneously computing derivatives, we store the dependencies of the expression tree in memory. Then, after completion of the forward pass, we compute partial derivatives of the output with respect to the intermediate variables, quantities known as **adjoints**, which we'll denote with \( v \bar \). To obtain the adjoint \( v \bar_i \) for a particular node, we look at each of the node's children, multiply the adjoint of the child by the partial derivative of the child with respect to \( v_i \), and then take the sum of these products. So, \( v_i \)'s contribution to the final output is determined both by how each of its children affect the output and how it affects each of its children. At the end, we obtain partial derivatives with respect to each input, so the gradient is computed with just a single execution of reverse mode autodiff, making it far better suited to the typical optimization setting in machine learning. In the context of neural networks, the **backpropagation algorithm**, which is used to compute derivatives with respect to network weights, may be viewed as a special case of reverse mode autodiff, where the adjoints with respect to intermediate layer activations are propagated backwards through the network. For general vector-valued functions, reverse mode produces one row of the Jacobian at a time, making it ideal when we have few outputs relative to inputs. Now, for both forward and reverse mode, what's especially neat is that a single pass does not take much longer than evaluating the function itself. In fact, computing a single column of the Jacobian in forward mode or a single row in reverse mode is guaranteed to take less than six times the number of operations in the original function implementation. In practice, it tends to only be about two or three times. Reverse mode is usually a bit more memory intensive than forward; we have to store the values of intermediate variables and their dependencies in memory. Various techniques have been developed that help make this more efficient, including **re-materialization**, where only a subset are stored and the remainder are recomputed during the backwards pass. Forward and reverse mode are the two extremes of automatic differentiation, but in some settings, a **hybrid approach** is actually preferred. For example, in second-order optimization, where information about an objective function's curvature is taken into account, a **Hessian-vector product** is sometimes needed. A reverse-on-forward version of autodiff allows efficient computation of this product. First, we use forward mode to compute the directional derivative \( \nabla f \cdot v \) by setting \( x \cdot \) to \( v \) as we did before. Then, reverse mode is used to differentiate again, resulting in the Hessian times \( v \). As with the Jacobian-vector product, we're able to compute the Hessian-vector product without explicitly computing the Hessian matrix itself. In general, we can compute arbitrarily higher-order derivatives by composing multiple executions of autodiff together. So, automatic differentiation helps make life much easier when we need to obtain derivatives of complicated functions. It's not always applicable, but when we can directly implement a function of interest in code, this set of techniques allows accurate computation of its derivatives with minimal overhead. Autodiff has a rich history, and ongoing research continues to improve it. Check out the links in the description to learn more. Thanks for watching!
Залогинтесь, что бы оставить свой комментарий